Summary
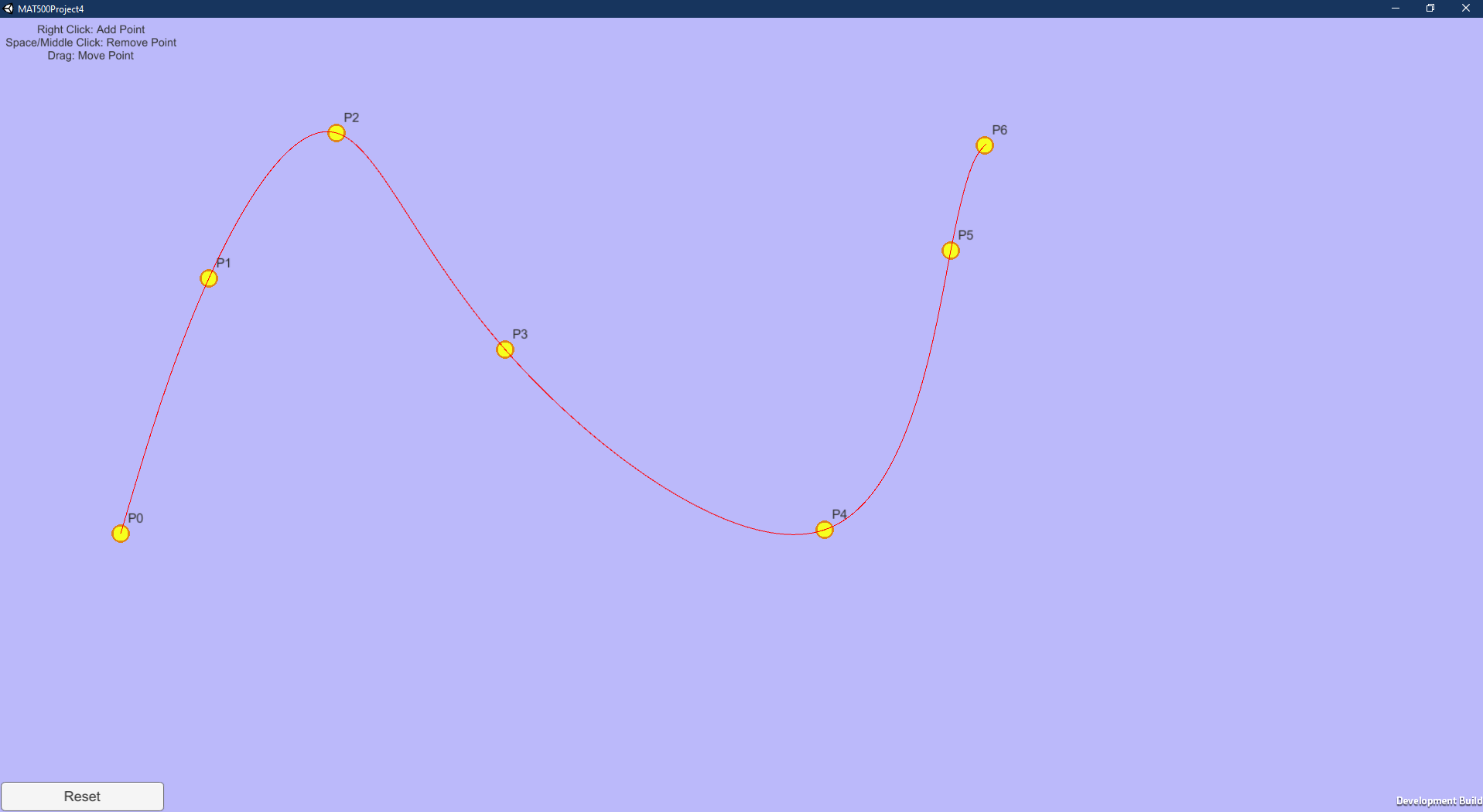
During my Master's degree, I built a framework to allow users to generate polynomials, Bezier curves, or B-splines in real-time based on input points. Users can add or remove points, and can even drag the points around.
Take a look at the code: github.com/aseemapastamb/MAT500
The framework was made in Unity, and it really helped me understand the math behind the curves. The optimization process to make the project run smoothly, even at higher degrees, was a fun challenge.
Project Snippets
Project 1
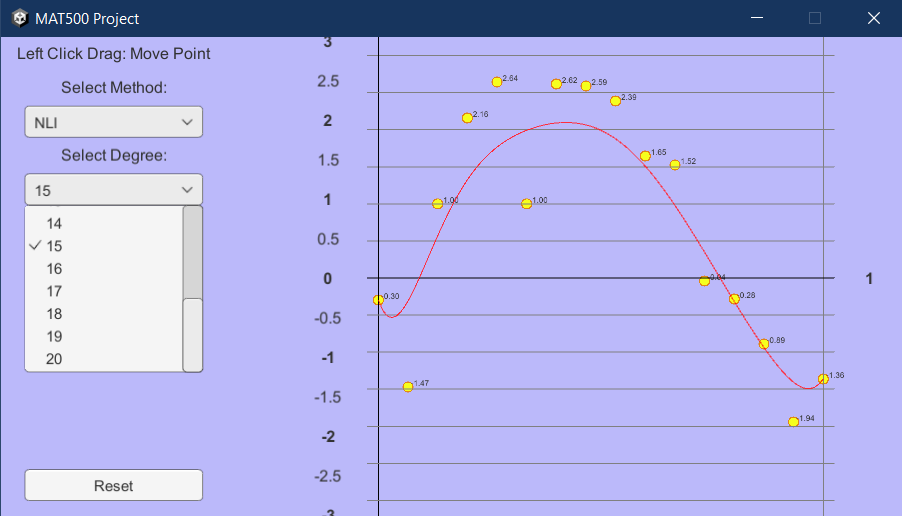
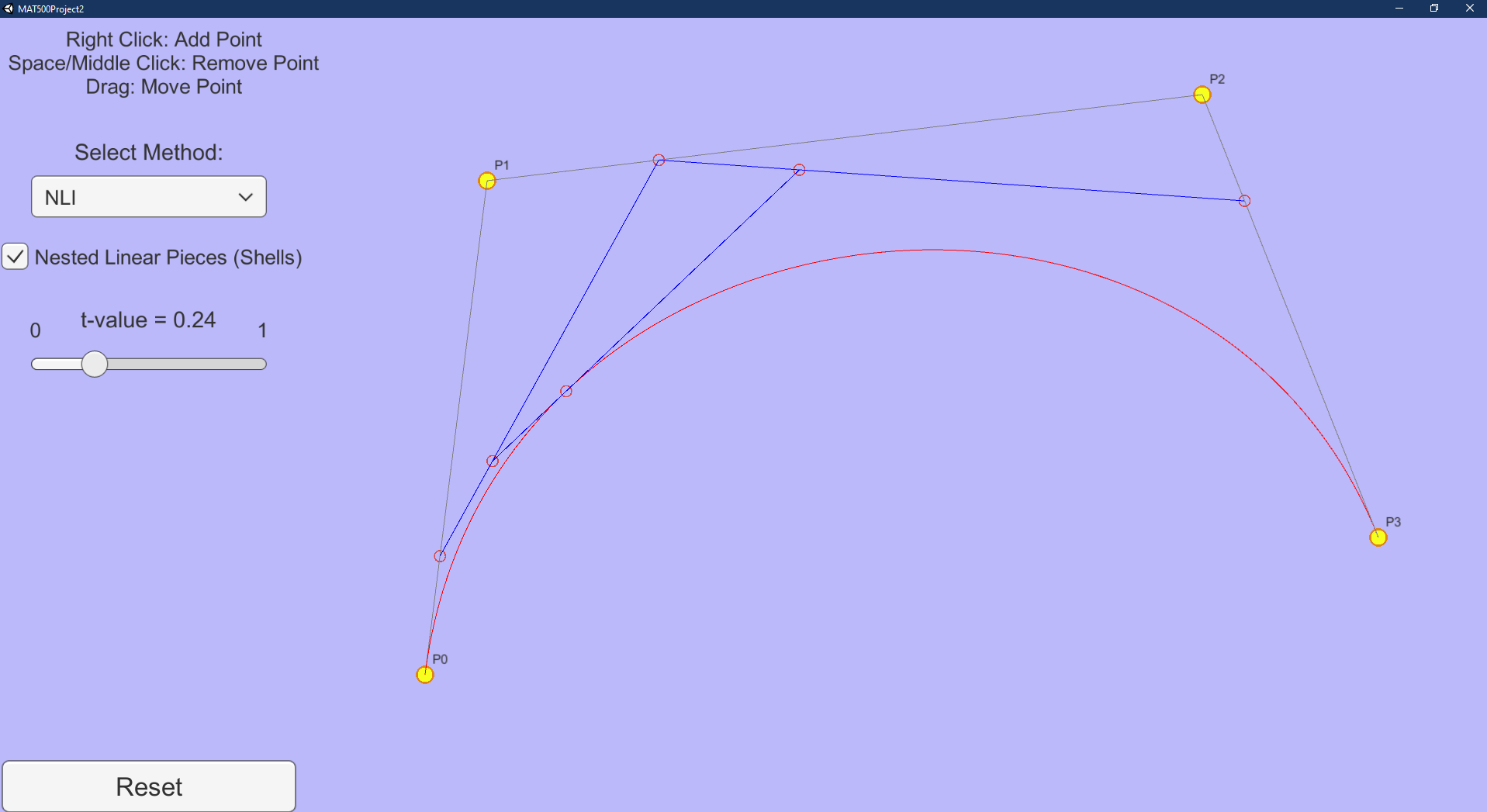
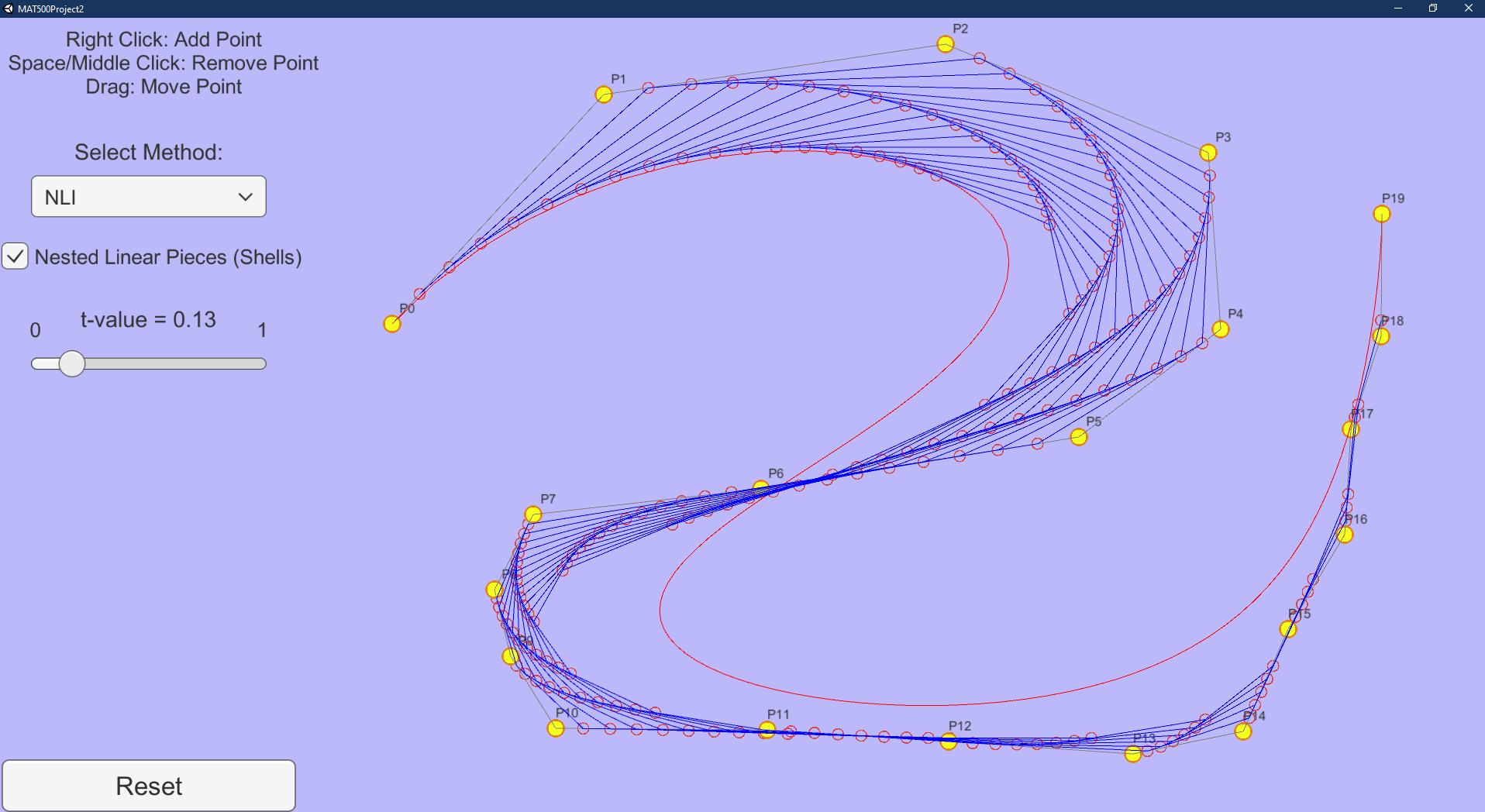
De Casteljau Algorithm for Polynomial Functions
This project demostrates how the coefficients of Bernstein polynomials affect the shape of a polynomial graph.
The dropdown menu allows the choice of NLI or BB-form.
NLI: Nested Linear Interpolation or the De Casteljau algorithm. BB-form: Berstein Basis form, which is the sum of Bernstein polynomials.
The degree dropdown offers a choice of d from 1 to 20, with the default being 1.
Project 2
De Casteljau Algorithm for Bezier Curves
Now, along with NLI and BB-form, a third method called Midpoint Subdivision is added.
The points are also now free to move anywhere.
The blue lines are called "shells". They are calculated using the "t-value" slider.
Project 3
Interpolating Polynomials
The curve is a parametric polynomial that actually passes through the points.
The calculation is done using a method called "Newton Form".
Project 4
Interpolating Cubic Splines
A cubic spline gives a much smoother curve than a polynomial.
A linear system is set up using the standard basis spline functions.
